Experiments in Reverse Engineering COBOL codebases

Avishek Sen Gupta on 10 August 2024

---

This post has not been written or edited by AI.

We will be talking about techniques in abstract, but will refer to concrete implementations in Cobol-REKT as needed.

Contents

• Introduction
• Parser
• Control Flow Graph (early version)
• Intermediate representation
  • Translation into Syntax Tree
  • Translation into Control Flowgraph
    • Identifying Procedural Structures
• Interpretation
  • Types of interpretation
• Control Flow Analysis
  • What is reducibility?
  • Tests for reducibility
  • Dominator analysis
  • Identifying irreducible regions
    • Strongly connected components analysis
    • DJ Graphs
  • Future work: Controlled Node Splitting
• Semantics-preserving tree transformations
  • Eliminating GOTOs
• Replicating COBOL’s record-based layout system
• References

Introduction

The source code for all of this work is based on Cobol-REKT.

Parser

The parser is the easier part, if only because I reused what was already available. The COBOL Language Support extension contains an ANTLR grammar which works. Note that it has been en

Control Flow Graph (early version)

A very naive version of a flowgraph can be built which is still tied to COBOL constructs. The nodes in this flowgraph represent native COBOL constructs. These nodes were originally designed to represent COBOL code as visual flowcharts, like below:

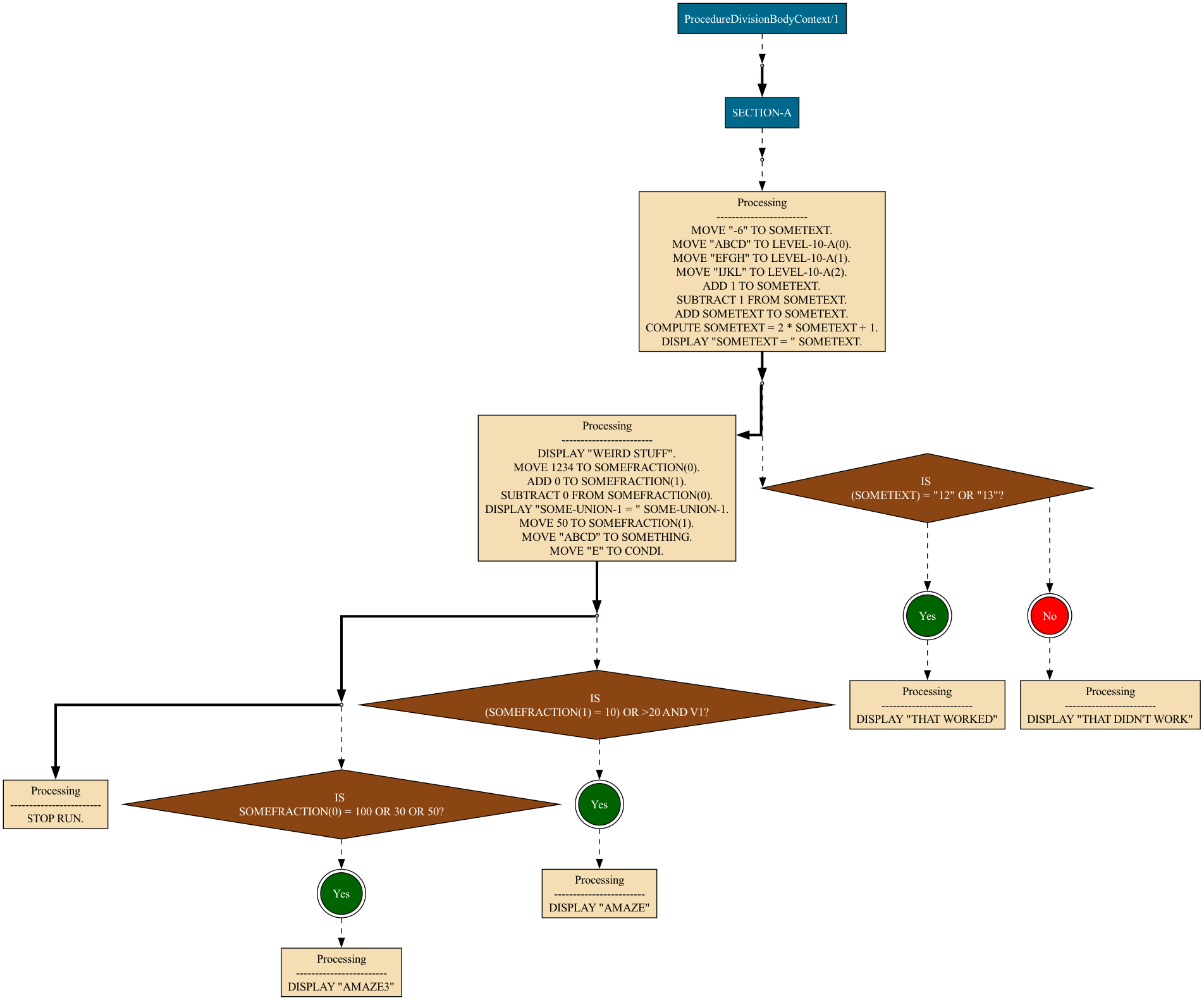
These nodes did not necessarily represent control flow very accurately, because of the following:

• There were always straight-line causal connections between every COBOL sentence. This included statements which unambiguously jumped to other sections/paragraphs of the program. This is because se

The syntax tree is also used for the following purposes:

• Building high-level flowgraph for further input into the intermediate representation
• Building symbol table with appropriate types
• Interpreting using a tree-walk interpreter
• External program dependency tracing

Intermediate representation

Translation into Syntax Tree

A more language-agnostic way of representing control flows (as well as syntax), is to decompose all COBOL-specific constructs into some simple intermediate representation which is more or less well-supported in most structured programming languages. Examples of such constructs would be:

• IF...THEN...ELSE
• SET
• LOOP (can represent normal loops, WHILE, and DO...WHILE constructs)

The LOOP semantic provides a nice way to encapsulate the semantics of different kinds of loops:

• WHILE-like constructs only have a termination condition and a ConditionTestTime attribute set to BEFORE.
• DO...WHILE-like constructs only have a termination condition and a ConditionTestTime attribute set to AFTER.
• Loop-like constructs only have an initial value, a maximum value, a loop update expression, and a ConditionTestTime attribute set to BEFORE.

A couple of examples of this translation process are shown below.

Translating EVALUATE

EVALUATE TRUE ALSO TRUE
              WHEN SCALED + RESULT < 10 ALSO INVOICE-AMOUNT = 10
                MOVE "CASE 1" TO SOMETHING
              WHEN SCALED + RESULT > 50 ALSO
                INVOICE-AMOUNT = ( SOMETEXT + RESULT ) / SCALED
                MOVE "CASE 2" TO SOMETHING
              WHEN OTHER
                MOVE "CASE OTHER" TO SOMETHING
            END-EVALUATE

This becomes:

if(and(eq(primitive(true), lt(add(ref('SCALED'), ref('RESULT')), primitive(10.0))), eq(primitive(true), eq(ref('INVOICE-AMOUNT'), primitive(10.0))))) 
 then 
{
	CODE_BLOCK: CODE_BLOCK: set(ref('SOMETHING'), value(primitive("CASE 1"))) 
}
 
else 
{
	if(and(eq(primitive(true), gt(add(ref('SCALED'), ref('RESULT')), primitive(50.0))), eq(primitive(true), eq(ref('INVOICE-AMOUNT'), divide(add(ref('SOMETEXT'), ref('RESULT')), ref('SCALED')))))) 
	 then 
	{
		 CODE_BLOCK: CODE_BLOCK: set(ref('SOMETHING'), value(primitive("CASE 2"))) 
	}
	 
	else 
	{
		 CODE_BLOCK: CODE_BLOCK: set(ref('SOMETHING'), value(primitive("CASE OTHER"))) 
	}
}

Translating PERFORM INLINE

PERFORM TEST BEFORE VARYING SOME-PART-1 FROM 1 BY 1
UNTIL SOME-PART-1 > 10
AFTER SOME-PART-2 FROM 1 BY 1 UNTIL SOME-PART-2 > 10
    DISPLAY "GOING " SOME-PART-1 " AND " SOME-PART-2
END-PERFORM.

This becomes:

loop[loopVariable=ref('SOME-PART-1'), initialValue=primitive(1.0), maxValue=NULL, terminateCondition=gt(ref('SOME-PART-1'), primitive(10.0)), loopUpdate=primitive(1.0), conditionTestTime=BEFORE] 
{
	loop[loopVariable=ref('SOME-PART-2'), initialValue=primitive(1.0), maxValue=NULL, terminateCondition=gt(ref('SOME-PART-2'), primitive(10.0)), loopUpdate=primitive(1.0), conditionTestTime=BEFORE] 
	{
		CODE_BLOCK: print(value(primitive("GOING ")), value(ref('SOME-PART-1')), value(primitive(" AND ")), value(ref('SOME-PART-2')))
	}
}

The translation process results in the intermediate syntax tree expressed in this intermediate form. Everything is converted into intermediate instructions. Note that GO TO statements carry over as JUMP statements; thus, the resulting intermediate program may still not be well-structured enough to be expressible in a modern progreamming language.

Translation into Control Flowgraph

The flowgraph is created from the intermediate syntax tree with a few salient points to note:

• Every instruction is represented by 3 separate sentinel instructions: ENTER, EXIT, and BODY. These are useful when dealing with branching statements or when delineating sections of code which are COBOL sections or paragraphs.
• Control flow edges are added only as needed, and not indiscriminately as in the earlier version of the flowgraph.
• Subroutine calls result in one outgoing edge from the call instruction BODY to the ENTER instruction of the start routine, and one incoming edge from the EXIT instruction of the end routine (which can be the start routine itself) to the EXIT instruction of the call instruction. The diagram below shows this scheme (the dotted arrow doesn’t actually exist).

flowchart TD TJ_ENTRY["[ENTER] jump(subroutine-1)"] TJ_BODY["[BODY] jump(subroutine-1)"] TJ_EXIT["[EXIT] jump(subroutine-1)"] T2["..."] TS1_ENTRY["[ENTER] subroutine-1"] TS1_BODY["[BODY] subroutine-1"] T3["..."] TS1_EXIT["[EXIT] subroutine-1"] TJ_ENTRY --> TJ_BODY TJ_BODY -.-> TJ_EXIT TJ_EXIT --> T2 TJ_BODY --> TS1_ENTRY TS1_ENTRY --> TS1_BODY TS1_BODY --> T3 T3 --> TS1_EXIT TS1_EXIT --> TJ_EXIT

Control Flow Analysis

In compiler theory, control flow analysis is usually done for the purposes of enabling various code optimisations and transformations. One way this is done is by identifying control structures in code which are not immediately apparent. For example, loops made out of IFs and GOTOs can be identified and such apparently ‘unstructured’ code can be transformed into structured programming constructs.

In the context of reverse engineering, we use control flowgraphs for the following:

• Determining reducibility
• Determining unambiguously-independent testable units
• Visualising implicit loops
• Determining reaching conditions

Such transformations are made easier when flowgraphs have a property called reducibility. There are several equivalent characterisations of flowgraphs. They are all explained in some depth here, but I’ll attempt to sim

Basic Blocks

Basic Blocks are useful for analysing flow of the code without worrying about the specific computational details of the code. They are also useful (and the more pertinent use-case in our case) for rewriting / transpiling potential unstructured COBOL code (code with possibly arbitrary GOTOs) into a structured form / language (i.e., without GOTOs).

The concept of a ‘natural loop’

flowchart TD T0["Instruction 0"] T1["Instruction 1"] T2["Instruction 2"] T3["Instruction 3"] T4["Instruction 4"] T5["Instruction 5\nIf (SOME-CONDITION) JUMP(T1)"] T6["Instruction 6"] T0 --> T1 T1 --> T2 T2 --> T3 T3 --> T4 T4 --> T5 T5 --> T1 T5 --> T6

Intuitively, we can see

Depth First Tree Ordering

Dominators and Immediate Dominators

Strongly Connected Components

Improper Loop Heuristic using Strongly Connected Components

Strongly Connected Components in a flowgraph represent the most general representation of looping constructs. Proper SCC’s have only one node in them that can be the entry point for any incoming edge from outside the SCC. These are natural loops. Having multiple entry points implies that there are arbitrary jumps into the body of the loop from outside the loop, which makes the loop improper, and consequently the graph, irreducible.

It is important to note that even if no improper SCC’s are detected, it does not imply that the flowgraph is reducible. See the flowgraph built in counterExample() in ReducibleFlowgraphTest for an example of such pathological graphs.

Proper SCC’s are a necessary condition for a reducible flowgraph, but not a sufficient condition. The sufficient condition is that no strongly connected subgraph be improper. However, SCC’s are maximal strongly connected subgraphs, which means they can contain improper strongly connected subgraphs inside them, which is why the distinction is important.

This is, however, a good test which can surface loop-specific reducibility problems. The test is done using the IrreducibleStronglyConnectedComponentsTask task.

Strongly Connected Components are detected using JGraphT’s built-in Kosarajau’s algorithm for finding SCC’s.

Improper Loop Body Detection

[TODO]

Reducibility

Take the following Cobol program as an example.

       IDENTIFICATION DIVISION.
       PROGRAM-ID. HELLO-WORLD.
       DATA DIVISION.
           WORKING-STORAGE SECTION.
               01  CONDI         PIC X VALUE "E".
                    88 V1      VALUE "E".
                    88 V2      VALUE "F".
       PROCEDURE DIVISION.
       SECTION-0 SECTION.
        P1.
            DISPLAY "Node 1".
        P2.
            IF V1
                DISPLAY "V1 IS TRUE, GOING TO Node 3"
                GO TO P3
            ELSE
                DISPLAY "V1 IS TRUE, GOING TO Node 4"
                GO TO P4.
        P3.
            IF V1
                DISPLAY "V1 IS TRUE, GOING TO Node 2"
                GO TO P2
            ELSE
                DISPLAY "V1 IS TRUE, GOING TO Node 4"
                GO TO P4.
        P4.
            IF V1
                DISPLAY "V1 IS TRUE, GOING TO Node 2"
                GO TO P2
            ELSE
                DISPLAY "V1 IS TRUE, GOING TO Node 3"
                GO TO P3.
        P5.
           DISPLAY "EXITING..."
           STOP RUN.

The above program, after conversion to Basic Blocks, gives a flowgraph which contains no improper Strongly Connected Components, but is still irreducible.

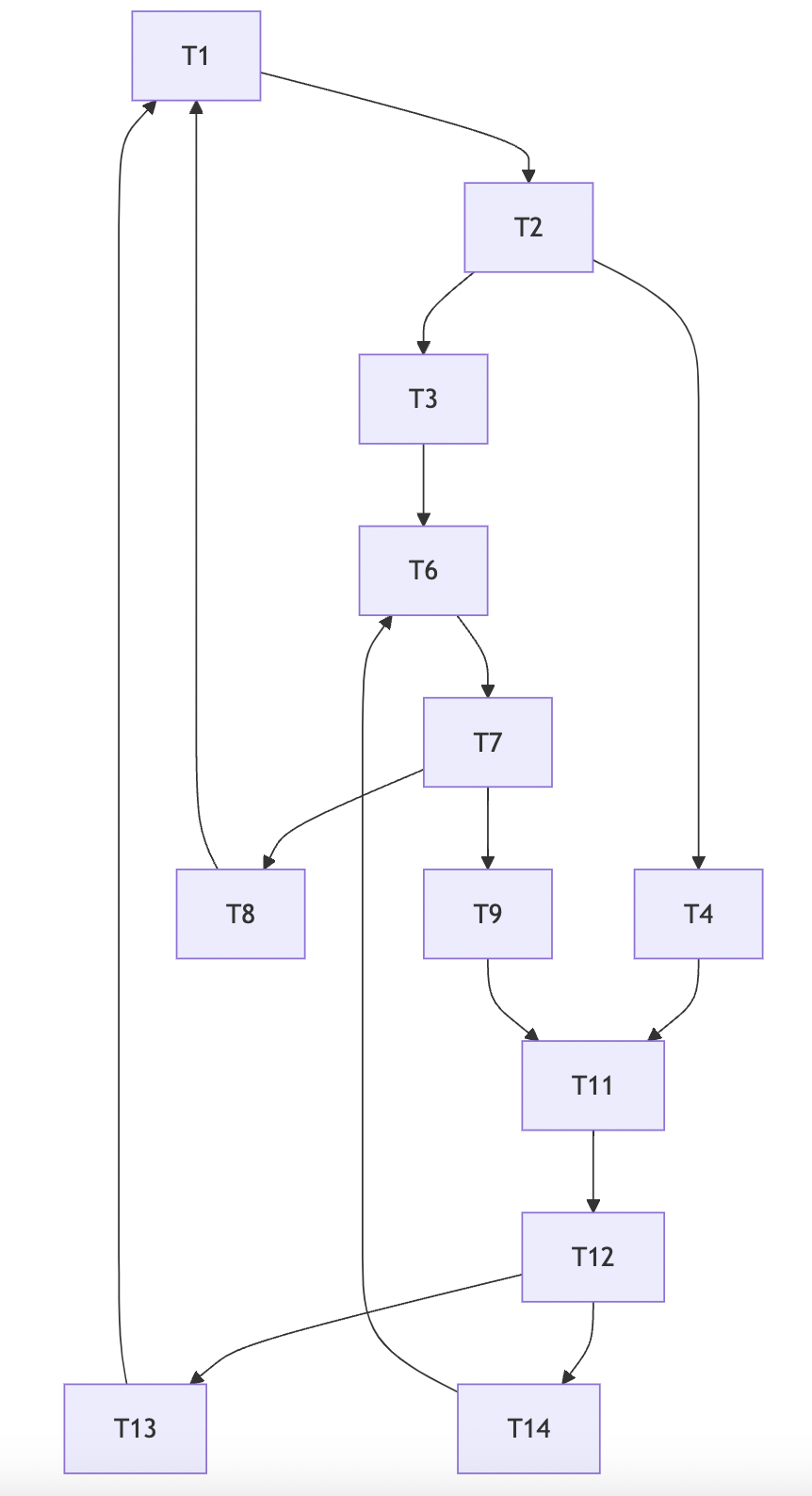
When this flowgraph is reduced via T1-T2 transformations, the limit flowgraph looks like the one below.

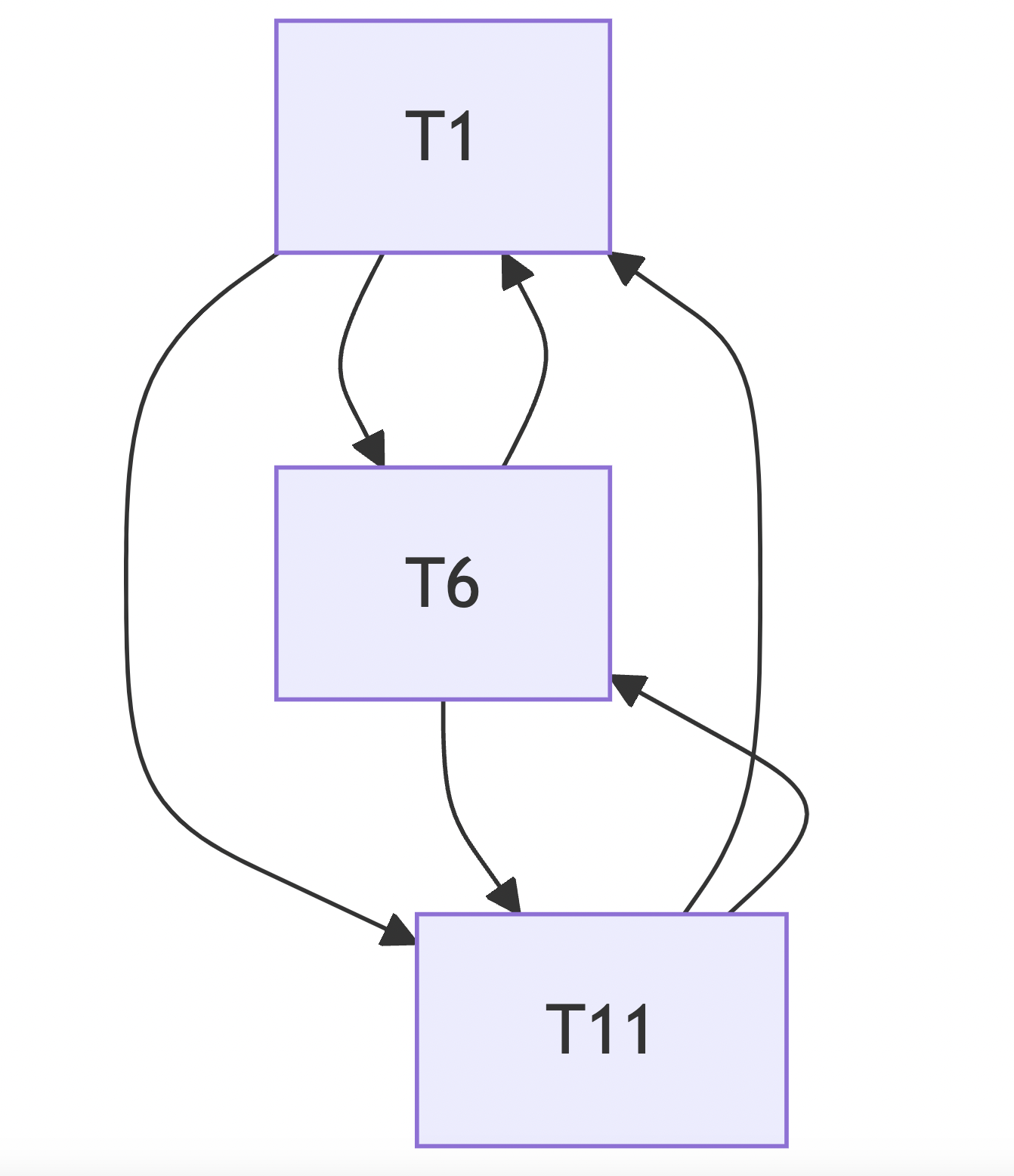
This is because the entire graph is a Strongly Connected Component (you can reach any node from any other node), but there are (non-maximal) strongly connected subgraphs which have multiple entry points. For example, T6 and T11 are strongly connected (and thus a loop), but have multiple entry points from T1, which is outside of this strongly connected subgraph (T6 is entered via T1, and T11 is entered via T1).

Moral of the story: No improper Strongly Connected Components do not guarantee a reducible flowgraph.

How does GnuCOBOL handle PERFORM?

Take the following simple program stop-run.cbl.

       IDENTIFICATION DIVISION.
       PROGRAM-ID.    STOPRUN.
       AUTHOR.        MOJO
       DATE-WRITTEN.  SEP 2024.
       ENVIRONMENT DIVISION.
       DATA DIVISION.
       WORKING-STORAGE SECTION.

       PROCEDURE DIVISION.
       S SECTION.
       SA1.
           DISPLAY "SA1".
           PERFORM SZ1.
       SE1.
           DISPLAY "SE1".
           STOP RUN.
       SZ1.
           DISPLAY "SZ1".
       SZ2.
           EXIT.

When compiled to produce the C source (run cobc -C stop-run.cbl), you can inspect the (generously annotated) file to find this gem:

  /* Line: 13        : PERFORM            : stop-run.cbl */
  /* PERFORM SZ1 */
  frame_ptr++;
  frame_ptr->perform_through = 6;
  frame_ptr->return_address_ptr = &&l_8;
  goto l_6;
  l_8:
  frame_ptr--;

That’s right, it compiles it to a goto with some context information (return label, for example) in the frame_ptr which is used at the end of SZ1 label like so:

  /* Line: 17        : Paragraph SZ1                     : stop-run.cbl */
  l_6:;

  /* Line: 18        : DISPLAY            : stop-run.cbl */
  cob_display (0, 1, 1, &c_3);

  /* Implicit PERFORM return */
  if (frame_ptr->perform_through == 6)
    goto *frame_ptr->return_address_ptr;

Unordered Notes

• GraalVM duplicates loop bodies. See here.
• Interesting research directions
  • Validate through control flow analysis + automated theorem provers the code generated by LLMs by testing control flowgraph equivalence, data flow analysis, etc. You can do this incrementally (per function, etc.) and augment it with guided human refactorings and generated tests.
  • Express source logic as facts in a reasoning engine which is fed as deterministic input to the LLM.

References

• Books
  • Advanced Compiler Design and Implementation by Steven Muchnik
  • Compilers: Principles, Techniques, and Tools by Aho, Sethi, Ullman
• General Overview
  • Structured Program Theorem
  • Control Flow Analysis slides
• Structural Transformations
  • Taming Control Flow: A Structured Approach to Eliminating Goto Statements
  • Solving the structured control flow problem once and for all
• COBOL-specific refactoring
  • Automatic compiler restructuring of COBOL programs into a proc per paragraph model - Patent US5778232A (Expired 2016)
  • Identifying Procedural Structure in Cobol Programs
• Dominator Algorithms
  • Graph-Theoretic Constructs for Program Control Flow Analysis - Allen and Cocke
  • A Fast Algorithm for Finding Dominators in a Flowgraph - Lengauer and Tarjan
  • A very readable explanation of the Lengauer-Tarjan algorithm
  • Algorithms for Finding Dominators in Directed Graphs
  • Dominator Tree Certification and Independent Spanning Trees
• Reducibility
  • Making Graphs Reducible with Controlled Node Splitting
  • Eliminating go to’s while Preserving Program Structure
  • No More Gotos: Decompilation Using Pattern-Independent Control-Flow Structuring and Semantics-Preserving Transformations
  • Identifying Loops Using DJ Graphs
  • No improper Strongly Connected Components does not imply Reducibility
• COBOL References
  • Examples: numeric data and internal representation
  • Enterprise Cobol for Z/OS 6.4 - Language Reference
  • GnuCOBOL Manual

---